Фрактал
В каждом человеке заложена природная любознательность, стремление познавать окружающий его мир. И в этом стремлении человек старается придерживаться логики в суждениях, анализируя процессы, происходящие вокруг его, человек стремится найти логичность происходящего и вывести некоторую закономерность. Самые большие умы на планете заняты этой задачей. Ученые ищут закономерность там, где ее быть не должно. Но, тем не менее, даже в хаосе можно найти связь между событиями. И эта связь фрактал.
Фрактал - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого. Фрактал это такой объект, для которого не важно , с каким усилением его рассматривать в увеличительное стекло, но при всех его увеличениях структура остается одной и той же.
Бенуа Мандельброт - отец фракталов
Бенуа Мандельброт - известный математик. Он ввел в научный обиход новое понятие "фракталы" (от латинского "fractus" , означающего "сломанный, разбитый" ) - самоподобные геометрические фигуры дробной размерности и показал их широчайшее распространение в природе, обществе, дав тем самым новое направление в развитии теории самоорганизации. Фракталы особенно привились в компьютерной математике, позволяющей визуально представить процесс их разворачивания в ходе итеративных (повторяющихся, самоприменимых) процедур. Мандельброт опубликовал свою работу в конце 1980 года, но объекты дробной размерности рассматривались математиками и ранее: Пьер Фату 1906, Ф. Рисс 1952, Дж. Хаббард 1976, Р. Брукс и Дж. Мателски 1976. Но это были только зерна, по разным причинам не давшие всхода. Именно с Мандельброта, оценившего весь масштаб открытия и связавшего его с компьютерами, фракталы начали самостоятельную жизнь.
Мандельброт - родился 20 ноября 1924 года в Варшаве, в еврейской семье из Литвы. Его семья переехала во Францию, когда Бенуа было 11 лет. Получил образование во Франции. В 1952 году в Сорбонне получил степень доктора математических наук. В 1958 году начал работать в научно-исследовательском центре IBM в Йорктауне, США.В середине 1960-х годов Мандельброт разработал то, что он назвал «фрактальная геометрия» или «геометрия природы». Целью фрактальной геометрии был анализ сломанных, морщинистых и нечетких форм.
Мандельброт использовал слово «фрактал» , потому что он предполагает осколочность и фракционность этих форм. Его величайшей работой считается книга «Фрактальная геометрия природы». Сегодня ученые пытаются расширить область фрактальной геометрии так, чтобы она могла быть применена практически ко всему в мире, от предсказания цен на рынке ценных бумаг до совершения новых открытий в теоретической физике. Мандельброт был профессором математических наук, почетным преподавателем Йельского Университета, Баттельским членом Тихоокеанской Национальной лаборатории.
Бенуа Мандельброта называют отцом фракталов и человеком, сумевшим покорить хаос. Он относился к той категории гениев, которые имеют уникальный талант лишь в одной сфере: Мандельброт обладал потрясающим воображением и мог представить отличные от привычного всем трехмерного пространства.
Площадь и длины фракталов
В евклидовой геометрии есть понятие размерности : размерность отрезка — единица, размерность круга — два, шара — три. Например, если мы будем измерять длину о
трезка, то, например, метровых отрезков в нём будет N, полуметровых 2N, дециметровых — 10N и так далее. В данном случае наблюдается прямая пропорциональная зависимость. В случае измерения площади мы уже получим следующие значения: 4N, 100N, то есть здесь зависимость уже квадратичная. Объём трёхмерных фигур пропорционален кубу их линейных размеров. Если попытаться применить эти правила к фрактальным объектам, возникает парадоксальная ситуация — их размерность окажется дробным числом. Так как фрактал состоит из бесконечного числа повторяющихся элементов, невозможно точно измерить его длину. Это означает, что чем более точным инструментом мы будем его измерять, тем большей окажется его длина. В то время как гладкая евклидова линия заполняет в точности одномерное пространство, фрактальная линия выходит за пределы одномерного пространства, вторгаясь в двумерное.
Таким образом, фрактальная размерность кривой Коха будет находиться между 1 и 2.Самым удивительным оказывается то, что и многие природные объекты обладают как бы дробной размерностью, хотя, строго говоря, для природных объектов такую размерность вычислить невозможно. Правильнее сказать, что в определённых диапазонах наблюдения природные объекты, возникшие в результате долгой диффузии и абсорбции, похожи на фрактальные множества. Например, размерность побережья лежит между 1,01 и 1,6, а кровеносной системы человека — между 3,4 и 3,6.
Практическое применение
Теория фракталов имеет практическое применение. Поскольку она тесно связана с визуализацией самоподобных образов, неудивительно, что первые, кто взял на вооружение алгоритмы и принципы построения необычных форм, — художники.
Фрактальные рисунки завораживают своими узорами. Они определенно напоминают изображения космических объектов — туманностей, скопления галактик и т.д. Поэтому вполне закономерно, что когда Мандельброт озвучил свою теорию фракталов, его исследования вызвали повышенный интерес у тех, кто занимался изучением астрономии
 |
 |
 |
Фрактальное сжатие изображений применяется в информатике. Первым и очевидным применением фрактальных алгоритмов стало так называемое фрактальное сжатие изображений. Фрактальное сжатие изображений — алгоритм сжатия изображений с потерями, основанный на применении систем итерируемых функций к изображениям. (Системы итерируемых функций или просто СИФ - представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое.)
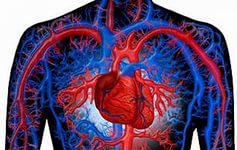
На данное время фракталы находят и, вероятно, будут находить применение в медицине. Сам по себе человеческий организм состоит из множества фракталоподобных структур: кровеносная система, мышцы, бронхи и т.д.
В физике фракталы применяются ещё шире. Например, в физике твёрдых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твёрдых, пористых, губчатых тел, различных аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами.